How many bytes does it take to make a good hash? Part Two.

Following up with a larger dataset

In my last post I discussed the use of a two stage hash as an optimisation to to determining file uniqueness. Given some empirical results I set about formalising my question and providing an answer based on inspection of a local dataset. However, in the interim I’ve gained access to a larger machine and a larger dataset. This time around I’ll be looking at ~290,000 files totalling in ~2.5TB. For reference the prior post looked at ~13,000 files in 700GB. The nature of the dataset is the same; this is a collection of files downloaded from the internet for personal and work related use. The files include music, videos, games, source code, zips, rars, tars, word files, excel files, Libreoffice files, etc… For this post the tools in use are the same as they were in the last post and the graphs are a bit higher res than they were last post.

Files still tend to cluster.

First thing’s first; lets look at the dataset to get familiar. The stats from ddh are as follows

290406 Total files (with duplicates): 2442714410 Kilobytes
229231 Total files (without duplicates): 2287991875 Kilobytes
207225 Single instance files: 2167162786 Kilobytes
22006 Shared instance files: 120829089 Kilobytes (83181 instances)

Graphing file sizes we have

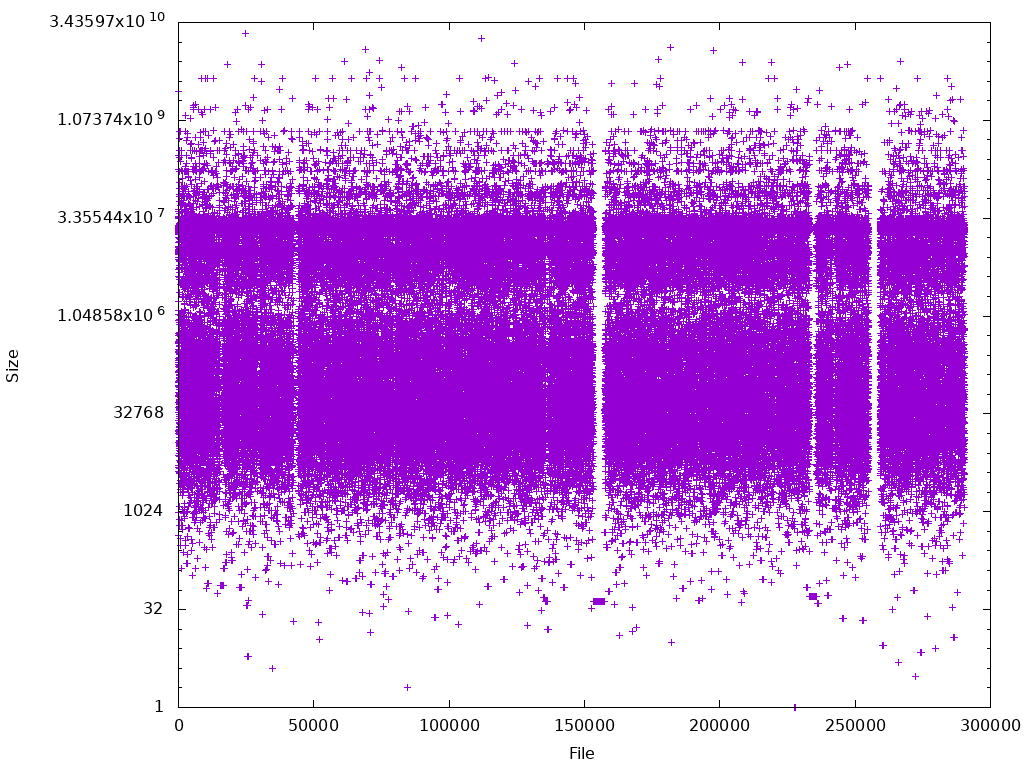
We can see files clustering as before with a much higher density. A higher resolution image is available here for those interested.

How to make a good hash with changing ingredients

We still have the same leading problem statement

How few bytes can we read and still differentiate most files?

But we’re not going to focus on that question in this post. In the last post we found 20 bytes to be sufficient, but with the shift in dataset a more useful question to investigate might be

Is 4KB sufficient to differentiate most files in most datasets?

Again we avoid defining the term most and work with an intuition for that term. The goal is to be confident in the choice of a 4KB first stage hash as 4KB maps well to modern storage systems. Proceeding as before we observe the following.

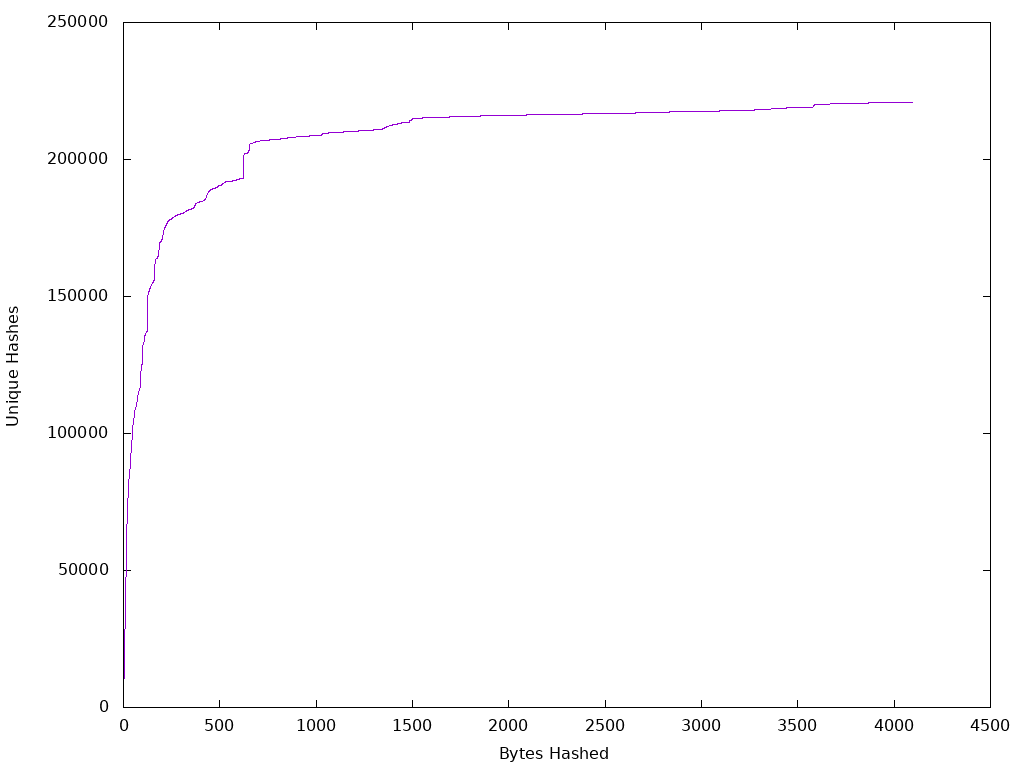
Again we see a point of diminishing returns, but for this dataset the point seems to be around 600 bytes. Perhaps this is unsurprising as more files increases the odds of any two files being similar for n bytes and indeed that is exactly what is shown here.

Satisfaction

This was a quick update, but it’s good to see that even with a large dataset 4KB provides a very good initial result. At the 600 byte mark there are 192,784 unique hashes out of 290,406 files of which 229,231 are unique. That’s 84% differentiation. Again 4KB is the smallest read we can do on modern storage and at 4KB we have 220,868 unique hashes. The 4KB first pass hash gives us 96% coverage of the unique files in the dataset. Considering the the simplicity of the solution 96% differentiation is just amazing.

Want to test your own dataset?

It’s clear that the point of diminishing returns will be unique for every dataset and if you’d like to see what your own dataset looks like you can find the code I use here file_compare.

This code does require that you have bash and gnuplot installed and the code doesn’t auto generate everything. Some manual inspection is required, but if you’re interested in going beyond what is done automatically feel free to reach out to me. If you’ve read both of my hashing posts you may have noticed that I skipped an image in this one. There’s a very good reason for that; the machine used for this post had 16GB of ram and making a gif out of all the individual plots resulted in a 33MB gif or a crashed gnuplot when flags for quality reduction were applied.

Thanks for reading