How many bytes does it take to make a good hash?
The Background
Over the past few months I’ve written a file duplicate finder ddh. Originally ddh was just a way to ease myself into the rust language, but as time progressed I became increasingly conscious of its performance and I set about the task of optimising. After a number of rewrites I got to the point where I was happy with the general structure:
1. Scan directories
2. Sort files by length
3. Hash files for which there is another of the same length
4. Sort by hash and display results as requested
This worked fine for some basic tests on my main system and after the performance work I had full system scans going in a few seconds. Brilliant! I’ve done a test and received a glowing result. Job done.
Job not actually done
Working with solid state storage is great, but testing on solid state storage alone can hide performance issues. In an effort to expose any unseen performance issues I continued testing with a collection of files stored on a spinning disk drive and I was lead to instant disappointment. In my first test I saw a runtime of 1h 30m. The full output was as follows
13262 Total files (with duplicates): 687907721 Kilobytes
12334 Total files (without duplicates): 683634507 Kilobytes
12168 Single instance files: 679372542 Kilobytes
166 Shared instance files: 4261965 Kilobytes (1094 instances)
The dataset was just under 700GB with about 13,000 files which gives some rough performance data showing about 132 Megabytes per second or the more interesting metric of about 3.8 files per second.
Why was ddh only getting through something like 3.8 files per second when there were only 1094 duplicates?
Files tend to cluster
Upon further analysis it became clear that the reason for the poor performance was that files (my files at least) tend to cluster in file sizes. What this means is that for some given file sizes there’s bound to be more demand on hashing than on other file sizes. In my case the issue is quite pronounced. In fact here’s a graph of the file sizes present in my dataset
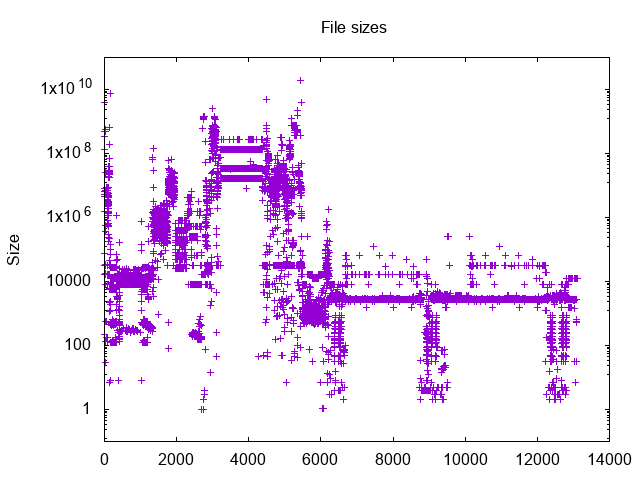
Interesting to know and really quite intuitive as well. So, there’s a simple solution here. Hash a small part of each file before comparing full file lengths. This changes the program logic from was was mentioned above to
1. Scan directories
2. Sort files by length
3. Pre Hash files for which there is another of the same length
4. Check for matching pre hashes and do a full hash on matches
5. Sort by hash and display results as requested
For the first implementation I used a pre hash size of 128KB for no reason other than I like that number. Rerun the spinning disk test on the same dataset and the runtime drops to 10 minutes. I also reran the test on my system drive and got a 1 second slowdown, but none the less; Fantastic! A bit of playing with the pre hash size and I was able to get the runtime down to about 5 minutes and this presented an interesting tradeoff; lower the pre hash size to reduce the time spent in step 3, but at the cost of increasing the time spent in step 5. So we come to the titular question; how many bytes does it take to make a good hash?
How to make a good hash
The problem statement at this point is
How many bytes of a file must be read to differentiate it from most other files?
or put another way
How few bytes can we read and still differentiate most files?
Ignoring the undefined term most it’s obvious that files which are duplicates will require full reads, but those are the degenerate cases which we ignore. The files we care about are the files which are different, but which may seem similar. File headers are bound to be similar, but then not all files have headers and some that have headers have potentially unique data in them. So, this is an easy enough question to answer with a little code, at least for a single dataset. Lets just hash all my files at one, two, three, etc… bytes and find out where we hit diminishing returns. Using my spinning disk dataset
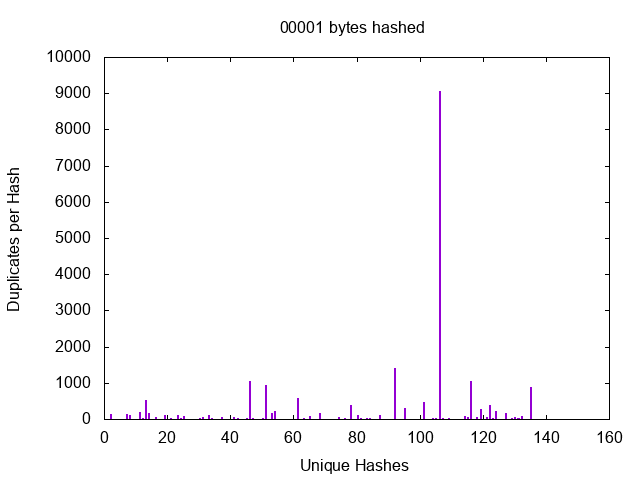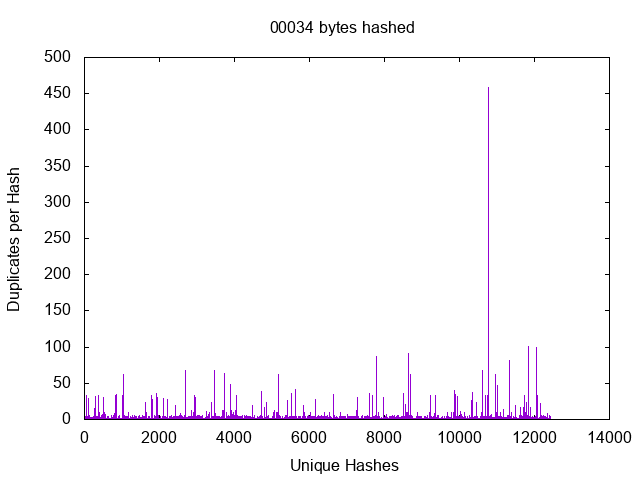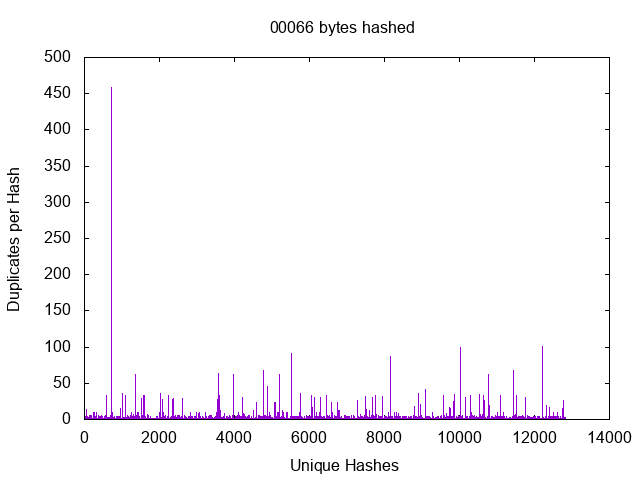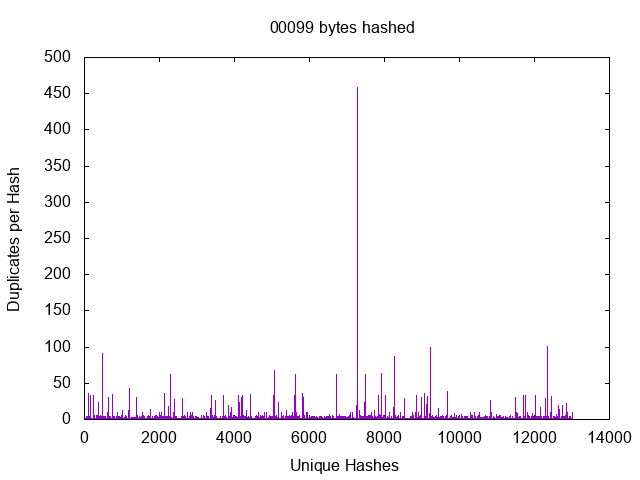
Here we see the number of files which match a given hash value for a number of bytes hashed.
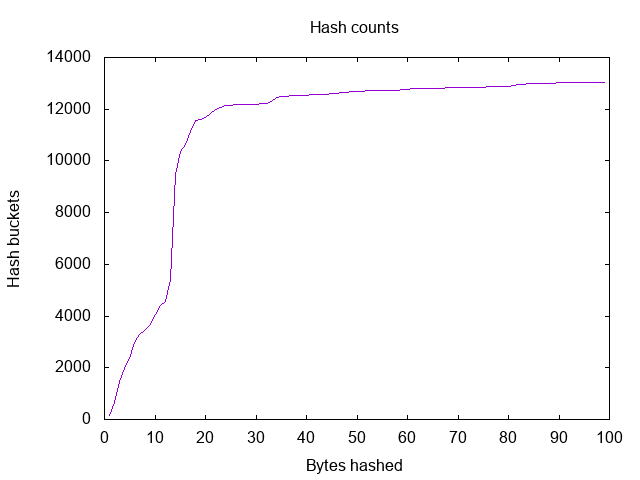
And here as a line graph
We can see a massive growth in the number of unique hashes starting at 13 bytes which makes my initial guess of 128KB look impressively wrong. When you think about it there are 8 bits to the byte and thus 2^104 possible 13 byte patters. It’s actually pretty shocking how many files were so similar in the 12 byte (2^96) space, but then it seems that files tend to cluster. It turns out that you can make a pretty good hash out of as few as 13 bytes and you will probably start hitting a point of diminishing returns by 20 bytes.
That’s good hash
At the onset the choice of pre hashing size seemed to be a choice of kilobytes, but as it turns out even one kilobyte is far in excess of what is really necessary. However, storage doesn’t actually give us access to one byte at a time. Storage gives us access to one block at a time and for modern storage systems one block is 4096 bytes. That is, the cost of reading 1 to 4096 bytes is the same. So given the nature of block storage the wise choice is to use all bytes given to us by our one read and to hash 4096 bytes.
Thanks for reading